Priorización 2023-2025: Aprendizajes Basales
MA2M OA 08
Mostrar que comprenden las razones trigonométricas de seno, coseno y tangente en triángulos rectángulos:
- Relacionándolas con las propiedades de la semejanza y los ángulos.
- Explicándolas de manera pictórica y simbólica, de manera manual y/o con software educativo.
- Aplicándolas para determinar ángulos o medidas de lados.
- Resolviendo problemas geométricos y de otras asignaturas.
Textos Escolares oficiales 2023
Actividades de apoyo pedagógico
Lecciones: clases completas
Evaluaciones del programa
Indicadores
Indicadores unidad 3
- -Dibujan triángulos rectángulos semejantes y los superponen en uno de sus ángulos para relacionar el ángulo con la proporción del cateto opuesto y la hipotenusa (respectivamente, el cateto adyacente y la hipotenusa).
- -Descubren que esta relación se mantiene para varios triángulos semejantes, y que el ángulo se mantiene.
- -Explican las razones trigonométricas por medio de dibujos.
- -Resuelven triángulos en ejercicios rutinarios; es decir, determinan todos sus ángulos y la medida de todos sus lados.
- -Resuelven problemas de la vida cotidiana, de geometría y de ciencias naturales, aplicando las razones trigonométricas.
Incorpora a tu evaluación las preguntas que te interesen pinchando "Agregar pregunta".
A la derecha aparecerá un número que indica la cantidad de preguntas seleccionadas. Pínchalo y podrás visualizarla accede al buscador del Banco de Preguntas
Preguntas
Buscando medidas de ángulos
Enunciado
En la siguiente figura se muestra un $\Delta ABC$, rectángulo en C:
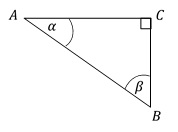
Si $tg (a) = \frac{1}{\sqrt{3}}$, ¿Cuál es la medida del $\measuredangle{\beta}$?
Alternativas
A) $30^\circ$
B) $45^\circ$
C) $60^\circ$
D) $90^\circ$
Calculando medidas
Enunciado
Sea el$\Delta EFG$. ¿Cuál es el valor de $\overline{EF}$?
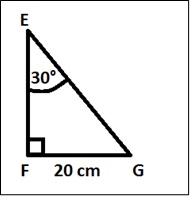
Alternativas
A) $20\; cm$
B) $20\sqrt{3}\; cm$
C) $\frac{20}{3}\sqrt{3}\; cm$
D) $60\; cm$
Elevando cometas
Enunciado
Carlos está volando un cometa y desea saber su altura. La sombra del cometa está a 8 metros de sus pies, y desde ahí, desde los pies, se puede observar el cometa con un ángulo de elevación de 60°. ¿Cuál es la altura alcanzada del cometa?
Alternativas
A) $8\sqrt{3}\; metros.$
B) $\frac{8\sqrt{3}}{3}\; metros.$
C) $24\sqrt{3}\;metros.$
D) $4\sqrt{3}\;metros.$
El sol y la sombra de un árbol
Enunciado
A cierta hora de la tarde, el sol proyecta sus rayos con un ángulo de depresión de 45°. ¿Cuánto mide la sombra que proyecta un árbol, de 12 metros de altura, en ese instante?
Alternativas
A) $6\sqrt{2} $ metros
B) 6 metros
C) $12\sqrt{2} $ metros
D) 12 metros
Aplicando razones trigonométricas
Enunciado
El siguiente $\Delta ABC$ es isósceles de base $\overline{AC}$ y $\overline{BD}$ es altura.
 |
¿Qué expresión permite calcular el valor del lado $\overline{AB}$
$\def\sen{\mathop{\mbox{\normalfont sen}}\nolimits}$
Alternativas
A) $ \Large \frac{32}{\cos 40^\circ}$
B) $ \Large \frac{sen 40^\circ}{16}$
C) $ \Large \frac{16}{sen 50^\circ}$
D) $ \Large \frac{16}{\cos 50^\circ}$
Relación entre lados y ángulos de un triángulo rectángulo
Enunciado
Observe el siguiente triángulo.
¿Cuál de las siguientes alternativas es falsa?
Alternativas
A) $tg\;{52}^\circ = \frac{b}{a}$
B) $\sen\;{38}^\circ = \frac{c}{a}$
C) $\cos 52^\circ = \frac{b}{a}$
D) $tg\; 38^\circ = \frac{c}{b}$
