Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA08 OA 10
Mostrar que comprenden la función afín:
- Generalizándola como la suma de una constante con una función lineal.
- Trasladando funciones lineales en el plano cartesiano.
- Determinando el cambio constante de un intervalo a otro, de manera gráfica y simbólica, de manera manual y/o con software educativo.
- Relacionándola con el interés simple.
- Utilizándola para resolver problemas de la vida diaria y de otras asignaturas.
Clasificaciones
Textos Escolares oficiales 2023

Matemática 8° básico, Santillana, Guía didáctica del docente Tomo 1

Matemática 8° básico, Santillana, Guía didáctica del docente Tomo 2
Actividades de apoyo pedagógico
Lecciones: clases completas
Evaluaciones del programa
Indicadores
Indicadores Unidad 2
- Representan, completan y corrigen tablas y gráficos pertenecientes a cambios con una base fija y tasa de cambio constante.
- Elaboran, basados en los gráficos, la ecuación de la función afín: f(x) = a • x + b.
- Determinan las regiones en el plano cartesiano cuyos puntos p(x,y) representan soluciones (x,y) de las inecuaciones: y <a • x + b o y > a • x + b.
- Diferencian modelos afines, lineales y de proporcionalidad inversa.
- Modelan situaciones de la vida diaria o de ciencias con funciones afines.
- Identifican, en la ecuación funcional, el factor a con la pendiente ∆y/∆y de la recta y el sumando b con el segmento entre el punto de intersección del gráfico con el eje vertical y el origen o(0,0)
- Elaboran gráficos de funciones afines a y b dadas o con dos puntos dados y verifican que las coordenadas de puntos pertenecientes al gráfico son soluciones de la ecuación f(x) = a • x + b.
- Resuelven problemas de la vida diaria o de ciencias que involucran el cambio constante expresado mediante ecuaciones recursivas de la forma f(x + 1) - f(x) = c.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Graficando funciones afines
Enunciado
¿Cuál de las siguientes gráficas representa a $\large y=5x-5$ ?
Alternativas
A)

B)

C)

D)

Respuesta
D)
De gráficos a ecuación
Enunciado
¿Cúal es el valor de $y$, considerando la siguiente función?
$f(x)= 3x+2$ con $x=\dfrac{1}{4}$

Alternativas
A) $y=\dfrac{4}{4}$
B) $y=\dfrac{3x}{4}$
C) $y=\dfrac{11}{4}$
D) $y=\dfrac{4}{11}$
Respuesta
C)
Para encontrar el valor de $y$ en función de $x$ consideramos la funcion que ya tenemos; es decir:
$f(x)= 3x+2;~\text{con}~x=\dfrac{1}{4}$
Por lo tanto:
$f(x)=3x+2$
$f(\dfrac{1}{4})=3x+2$
$f(\dfrac{1}{4})=\left(\dfrac{3}{1}\cdot\dfrac{1}{4}\right)+\dfrac{2}{1}$
$f(\dfrac{1}{4})=\dfrac{3}{4}+\dfrac{2}{1}$
$f(\dfrac{1}{4})=\dfrac{3+8}{4}$
$f(\dfrac{1}{4})=\dfrac{11}{4}$
Modelación de situaciones con funciones
Enunciado
Observa la figura:

¿Cuál es la expresión de la función afín?
Alternativas
A) $f(x)=2x+\dfrac{4}{3}$
B) $f(x)=-\dfrac{2}{3}x-\dfrac{4}{3}$
C) $f(x)=-\dfrac{2}{3}x-\dfrac{4}{3}$
D) $f(x)=-\dfrac{2}{3}x+\dfrac{4}{3}$
Respuesta
D
Debemos ubicar dos puntos de la función, por ejemplo, $(2,0)$ y $(-1,2)$.
Calculamos la pendiente:
$m=\dfrac{2-0}{-1-2}=-\dfrac{2}{3}$
Finalmente la ecuación de la recta es:
$f(x)=-\dfrac{2}{3}x+\dfrac{4}{3}$
Ecuaciones recursivas
Enunciado
¿Cuál de los siguientes gráficos representa a la función $f(x) = 2 - \dfrac{x}{2}$?
Alternativas
A)

B)

C)

D)

Respuesta
A
Veamos que el gráfico que corresponde con la función otorgada en el enunciado es el de la alternativa A). Esto debido a que contiene el punto $(0,2)$ ordenada en el origen y posee una pendiente negativa igual a $-\dfrac{1}{2}$.
Cambios de base fija y tasa de cambio constante
Enunciado
¿Qué función afín representa la gráfica?

Alternativas
A) $f(x)=1-\dfrac{2x}{5}$
B) $f(x)=1+\dfrac{2x}{5}$
C) $f(x)=1-\dfrac{5x}{2}$
D) $f(x)=1+\dfrac{5x}{2}$
Respuesta
A)
Veamos que:
$f(x)=1-\dfrac{2x}{5}$
- Para $x=0$ tenemos $f(0)=1$
- Para $x=5$ tenemos $f(5)=-1$
El poder del viento
Enunciado
Villazed está contemplando construir varias centrales de energía eólica para producir electricidad.

La municipalidad de Villazed recogió información sobre el siguiente modelo.
| Modelo | E-82 |
| Altura de la torre | $138$ metros |
| Número de paletas del rotor | $3$ |
| Longitud de una paleta del rotor | $40$ metros |
| Velocidad máxima de rotación | $20$ vueltas por minuto |
| Coste de construcción | $3200000$ zeds |
| Ingreso | $0,10$ zeds por kWh generado |
| Costo de mantención | $0,01$ zeds por kWh generado |
| Eficiencia | Operativa el $97\%$ del año |
Nota: El kilovatio-hora (kWh) es una unidad de medida de la energía eléctrica.
Villazed desea calcular los costos y la ganancia que generaría la construcción de esta central de energía eólica.
El alcalde de Villazed propone la siguiente fórmula para calcular el beneficio económico E (en zeds) durante una serie de años a, si construye el modelo E-82.

Según la fórmula del alcalde ¿cuál es el número mínimo de años de funcionamiento requeridos para cubrir los costos de construcción de la central de energía eólica?
Alternativas
A) $6$ años.
B) $8$ años.
C) $10$ años.
D) $12$ años.
Respuesta
B)
Vender periódicos
Enunciado

Juan decide solicitar un puesto de vendedor de periódicos. Tiene que elegir entre La Estrella de Zedlandia y El Diario de Zedlandia.
¿Cuál de los siguientes gráficos es la representación correcta de cómo pagan a sus vendedores los dos periódicos?
Alternativas
A)

B)

C)

D)

Respuesta
C)
Ecuaciones y sus gráficas
Enunciado
¿Cuál de las siguientes funciones está mejor representada en la gráfica adjunta?

Alternativas
A) f(x) = -x
B) f(x) = $\dfrac{1}{2}$x - 1
C) f(x) = -$\dfrac{1}{2}$x + 1
D) f(x) = -2x - 1
Respuesta
D
Como la gráfica es una recta la función correspondiente expresada algebraicamente, será $f(x) = mx + n$. Como corta al eje Y en el punto $(0, -1)\rightarrow n = -1$
Ya que la recta es decreciente, su pendiente es negativa; es decir, m < 0. Su valor lo podemos determinar gráficamente:
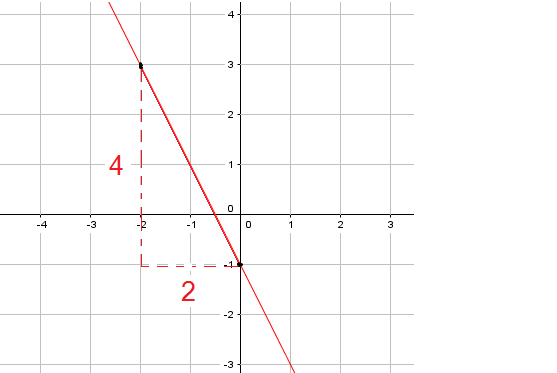
m = -$\dfrac{4}{2}$
m = -2
Por lo tanto, la gráfica corresponde a la función f(x) = -2x - 1.

















